CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals

Objective
To explore the similarities and differences between the different quadrilaterals like parallelogram, rectangle, rhombus and square with respect to their diagonals.

Prerequisite Knowledge
Properties of parallelogram, rectangle, square, rhombus.

  1. In parallelogram, diagonals are not equal.
  2. In rectangle, diagonals are equal.
  3. In rhombus, diagonals are not equal but bisect each other at 90°
  4. In square, diagonals are equal and bisect each other at 90°.

Materials Required
Glazed papers, ruler, a pair of scissors, pencil, tracing paper.

Procedure
Case I:

  1. Make a parallelogram on a glazed paper by paper folding and name it as ABCD. Join AC and BD.
  2. Draw and cut replicas of AABC and ABCD. Coincide the diagonals AC and BD.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 1
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 2
    Observation:
    We observe that diagonal AC ≠ diagonal BD.

Case II

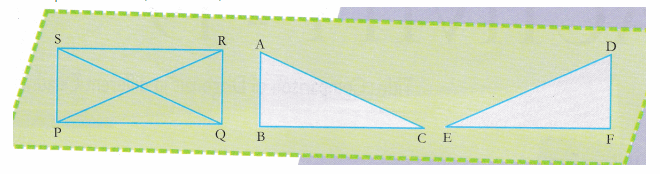
  1. Make a rectangle by paper folding on a glazed paper. Name it as PQRS. Join PR and QS.
  2. Cut replicas of ∆PQS and ∆PQR and name them as ∆BCA and ∆EFD.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 3
    3. Place two replicas such that AC and ED coincise eachother and side AB is opposite to side FD.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 4
    Observation:
    Here we notice that AC = DE. (as they overlap each other)
    ∴ diagonal AC = diagonal DE
    ∴ QS = PR

Case III:

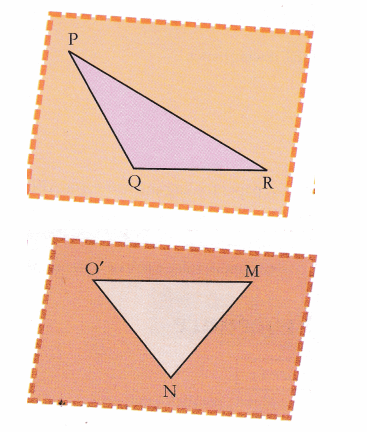
  1. Make a rhombus by paper folding on a glazed paper. Name it as ABCD. Join AC and BD.
  2. Draw and cut replicas of ∆ABC and ∆DCB and name them as ∆PQR and ∆MNO’ respectively.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 5
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 6
  3. Place two replicas such that PR and MO’ coincide each other.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 7
    Observation:
    We observe thatPR ≠ O’M.
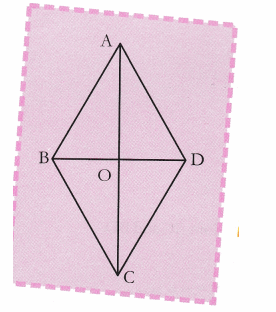
    ∴ diagonal AC ≠ diagonal BD
  4. Draw and cut replicas of ∆AOB and ∆BOC and verify the congruency of two triangles by placing one over other.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 8
    Here BC = AB
    OB = BO
    OC = OA
    ∴∆BOC = ∆BOA
    ∴∠BOC = ∠BOA
    ∴∠BOC + ∠BOA = 180° (linear pair angles)
    2∠BOC = 180° [from (i)]
    ∴ ∠BOC = 90°
    Thus, it is verified that in a rhombus, diagonals are not equal but bisect each other at 90°.

Case IV:

  1. Make a square by paper folding on a glazed paper. Name it as PQRS. Join PR and SQ.
  2. Draw and cut replicas of ∆PQS and ∆PQR.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 9
  3. Place two replicas along their diagonals SQ and PR. Here, we observe that both diagonals overlap each other completely. Thus, diagonal SQ = diagonal PR.
  4. Draw and cut replicas of ∆POQ and ∆POS. Place these replicas as shown in fig. below.
    CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 10
    Observation:
    Here, PQ = SP (sides of a square)
    OP = OP (common side)
    OQ = OS (By observation)
    ∆POQ = ∆POS (By SSS)
    ∴ ∠POQ = ∠POS (C.P.C.T.)
    But ∠POQ + ∠POS = 180° (linear pair angles)
    2∠POQ = 180°
    ∠POQ = 90°
    This implies that in a square, diagonals are equal and bisect each other at 90°.

Observation
By paper folding and cutting activity it is very much clear that rectangle, square, rhombus and parallelogram differ by their diagonal properties.
In parallelogram, diagonals are not equal, in rectangle diagonals are equal, in rhombus diagonals are not equal but bisect each other at 90°, in square, diagonals are equal and bisect each other at 90°.

Result
We verified that, in parallelogram diagonals are not equal, in square diagonals are equal and bisect each other at 90°. In rectangle diagonals are equal and bisect each other at 90°. In rhombus, diagonals are not equal but bisect at 90°. In this way these figures differentiate each other on the basis of their diagonals.

Learning Outcome
Though square, rectangle and rhombus all have the properties of parallelogram but they are different on the basis of their diagonals.

Activity Time
Draw all types of quadrilaterals on the same plane by using different glazed paper.
CBSE Class 9 Maths Lab Manual – Comparison of Diagonals in Different Quadrilaterals 11
Q – Quadrilateral
P – Parallelogram
Re – Rectangle
R – Rhombus
S – Square
We conclude that, all squares are rhombus, rectangle and parallelogram.

Viva Voce

Question 1.
What do you mean by a rectangle ?
Answer:
A parallelogram having one angle as 90°, is called a rectangle.

Question 2.
All squares are rectangles. Is it true ?
Answer:
Yes.

Question 3.
What is the main difference between a square and a rhombus ?
Answer:
In a square, diagonals are equal and in a rhombus, diagonals are not equal.

Question 4.
All squares are rhombuses. Is this true ?
Answer:
Yes.

Question 5.
All rhombus are squares. Is this true ?
Answer:
No.

Question 6.
What are main types of parallelogram ?
Answer:
Rectangle, square, rhombus.

Question 7.
What is the main difference between a rectangle and a square ?
Answer:
In a rectangle, opposite sides are equal and in a square all the four sides are equal.

Question 8.
How can you say that the parallelogram is a rectangle ?
Answer:
If in a parallelogram, one of the angles is 90°, then it becomes a rectangle.

Question 9.
Differentiate between a parallelogram and a rectangle.
Answer:
In a parallelogram, diagonals are not equal and in a rectangle, diagonals are equal.

Multiple Choice Questions

Question 1.
The similarity between a parallelogram and a rectangle in opposite sides are :
(i) equal and parallel
(ii) not equal
(iii) not parallel
(iv) none of these

Question 2.
The difference between a rectangle and a square is in square all sides are:
(i) equal
(ii) not equal
(iii) can’t say
(iv) none of these

Question 3.
Two sides of a parallelogram having no common end points are called its:
(i) diagonals
(ii) adjacent sides
(iii) opposite sides
(iv) none of these

Question 4.
A quadrilateral which has one pair of opposite sides parallel is called a:
(i) trapezium
(ii) square
(iii) rectangle
(iv) none of these

Question 5.
A quadrilateral in which two pairs of adjacent sides are of equal length is known as a:
(i) parallelogram
(ii) kite
(iii) trapezium
(iv) none of these

Question 6.
A diagonal of a parallelogram divides it into two triangles which are:
(i) congruent
(ii) not congruent
(iii) similar
(iv) none of these

Question 7.
In a parallelogram ABCD, if the length of a diagonal is 5cm and ∠ABC = 90°, then the length of other diagonal will be:
(i) 5 cm
(ii) 6 cm
(iii) 7 cm
(iv) none of these

Question 8.
In a parallelogram PQRS, PR and QS are equal and PQ = 6 cm. What is the length of RS ?
(i) 7 cm
(ii) 6 cm
(iii) 3 cm
(iv) none of these

Question 9.
What will be the area of a parallelogram whose base is 6cm and its corresponding altitude is 8cm ?
(i) 48 cm2
(ii) 40 cm2
(iii) 24 cm2
(iv) none of these

Question 10.
Lengths of the adjacent sides of a parallelogram are equal and intersect at 90° and length of the diagonal is 20cm. What is length of the side of the parallelogram?
(i) 2√5 cm
(ii) 5√4 cm
(iii) 10√2 cm
(iv) none of these

Answers

  1. (i)
  2. (i)
  3. (iii)
  4. (i)
  5. (ii)
  6. (i)
  7. (i)
  8. (ii)
  9. (i)
  10. (iii)

Math Lab ManualMath Labs with ActivityMath LabsScience LabsScience Practical Skills

Posted in CBSE  •