CBSE Class 9 Maths Lab Manual – Algebraic Identity (a2 – b2) = (a – b)(a + b)

CBSE Class 9 Maths Lab Manual – Algebraic Identity (a² – b²) = (a – b)(a + b)

Objective
To verify the identity a² – b² = (a + b)(a – b) by paper cutting and pasting.

Prerequisite Knowledge

1. Area of square = a², where side of a square = a.
2. Area of rectangle = l x b.

Materials Required
White sheets of paper, two glazed papers (pink and blue), a pair of scissors, geometry box, glues tick.

Procedure
Take any two distinct values of a and b (a > b) say a = 5 units, b = 3 units.

1. Draw a pink square of side 5 units and name it as ABCD as shown in fig. (i).
   
2. Draw a blue square of side 3 units and name it as EFGH as shown in fig. (ii).
   
3. Cut these squares from glazed papers.
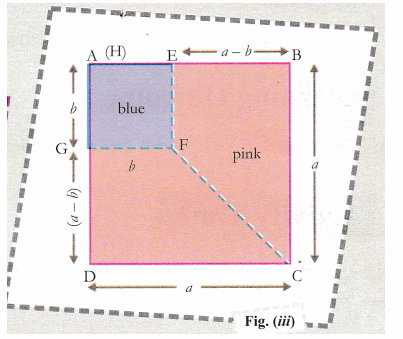
4. Paste two squares on a white sheet of paper. Square EFGH is pasted over square ABCD as shown in fig. (iii).
   
5. Join FC. Cut the pink portion along FC and dotted lines. We get two quadrilaterals as EFCB and GFCD.
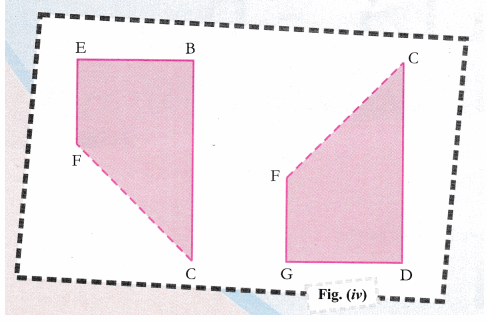
6. Now, place these two quadrilaterals on other white sheet of paper such that we get a rectangle. One piece of quadrilateral is reversed to other as shown in fig.(iv) and fig.(v).
   
   

Observation and Calculation
In fig. (i), area of square ABCD = a² = (5)² = 25 sq. units
fig. (ii), area of square EFGH = b² = (3)² = 9 sq. units
fig. (iii), area of quadrilateral EBCF + area of quadrilateral GFCD = area of ABCD – area of square EFGH
= (a² – b²) sq. units
= 25 – 9
= 16 sq. units … (i)
fig. (v), area of rectangle EDGB = EB x ED
= (a – b)(a+b)
= (5 – 3)(5 + 3)
= 2 x 8
= 16 sq. units … (ii)
From (i) and (ii), we have a² – b² = (a – b)(a + b)

Result
The identity (a² – b²) = (a + b) (a – b) is verified by paper cutting and pasting.

Learning Outcome
The identity (a² – b²) = (a+b)(a – b) is verified geometrically and can be verified by taking any other values of a and b.

Activity Time
Verify a² – b² = (a – b)(a + b) by two different coloured papers, by taking different values of a and b.
e.g., a = 7, b = 3

Viva Voce

Question 1.
Is (a² – b²) monomial?
Answer:
No, it is a binomial.

Question 2.
Write coefficient of x² in 49 – 4x².
Answer:
-4.

Question 3.
Write the factors of (x² – \(\frac { 1 }{ { x }^{ 2 } }\))
Answer:
(x + \(\frac { 1 }{ x }\))(x – \(\frac { 1 }{ x }\))

Question 4.
Simplify: (3 – 2x)(3 + 2x).
Answer:
9 – 4x².

Question 5.
Factorize: x² – \(\frac { { y }^{ 2 } }{ 100 }\)
Answer:
(x – \(\frac { y }{ 10 }\))(x + \(\frac { y }{ 10 }\))

Question 6.
Find the value of 95 x 105.
Answer:
Using the identity a² – b² = (a – b)(a + b),
95 x 105 may be written as (100 – 5)(100 + 5) = 100² – 5² = 10000 – 25 = 9975

Question 7.
Flow many zeroes are possible for x² – 4?
Answer:
2 zeroes, (2, -2).

Question 8.
Is x² – \(\frac { 1 }{ { x }^{ 2 } }\) a polynomial?
Answer:
No, as power of x in \(\frac { 1 }{ { x }^{ 2 } }\) is -2.

Question 9.
Write the coefficient of x² in 5 – 2x²
Answer:
-2.

Question 10.
Write the dimensions of a rectangle whose area is x² – 16.
Answer:
Dimensions are x – 4 and x + 4.

Multiple Choice Questions

Question 1.
Write the factors of 25x² -1:
(i) (5x – 1)(5x + 1)
(ii) (5x – 1)2
(iii) (25x – 1)(25x+ 1)
(iv) none of these

Question 2.
Find the factors of 49 – 81y²:
(i) (7 – 9y²)(7 + 9y²)
(ii) (7 + 9y) (7 – 9y)
(iii) (49 – y) (49 + y)
(iv) none of these

Question 3.
Write the zeroes of 36x² – 25:
(i) \(\pm \frac { 5 }{ 6 }\)
(ii) \(\frac { 5 }{ 6 }\)
(iii) \(-\frac { 5 }{ 6 }\)
(iv) none of these

Question 4.
Write the zeroes of 49 – 64b²:
(i) \(\frac { 7 }{ 8 }\)
(ii) \(\pm \frac { 7 }{ 8 }\)
(iii) \(-\frac { 7 }{ 8 }\)
(iv) none of these

Question 5.
Evaluate 124 x 116, using the identity (a² – b²) = (a + b) (a – b) :
(i) 14384
(ii) 14834
(iii) 14483
(iv) none of these

Question 6.
Find all the integral zeroes of polynomial p(x) =x² – 4:
(i) 4
(ii) -2
(iii) 2, -2
(iv) none of these

Question 7.
Is (x – 2) a factor of 49x² – 25:
(i) no
(ii) yes
(iii) can’t say
(iv) none of these

Question 8.
Find p(0) for p(x) = (x – 1)(x + 1):
(i) 1
(ii) 0
(iii) -1
(iv) none of these

Question 9.
Write the degree of the polynomial x² – 81:
(i) 3
(ii) 4
(iii) 81
(iv) none of these

Question 10.
Write the factors of x² – 64 :
(i) (x² – 4)(x² + 4)
(ii) (x² +8)(x – 2√2)(x + 2√2)
(iii) (x² + 8)(x² + 8)
(iv) none of these

Answers

1. (i)
2. (ii)
3. (i)
4. (ii)
5. (i)
6. (iii)
7. (i)
8. (iii)
9. (ii)
10. (ii)

Math Lab ManualMath Labs with ActivityMath LabsScience LabsScience Practical Skills